Моделирование фильтра на отрезках линии передачи
Второй пример иллюстрирует использование линии задержки как Z задерживающего звена при моделировании цифрового фильтра [11]. В этом примере демонстрируется использование идеальной линии передачи без потерь для моделирования рекурсивного цифрового фильтра [7.2] Баттерворта третьего порядка. Системная функция такого фильтра имеет вид:
H (z) = (0.156z-1 + 0.183z-2)/(1- 1. 081z-1 + 0.607z-2 - 0.123z-3) (6.1)
Структурная схема фильтра, соответствующая (6.1), показана на Рис. 6.8 [11]. С использованием линий передачи и структурных схем фильтров, пред-ставляемых на их основе, моделирование цифровых фильтров становится более простым и наглядным, чем использование системных функций и зависимых источников, задаваемых Z – преобразованием, особенно в учебном процессе.
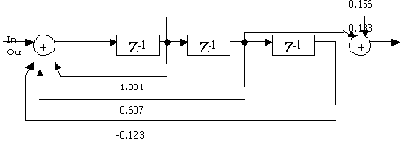
Рис. 6.8
Принципиальная схема фильтра, соответствующая Рис. 6.8, показана на Рис. 6.9. Отрезок идеальной линии передачи на Рис. 6.9 соответствует элементу z-1 на Рис. 6.8 и в системной функции (6.1) фильтра. Линия задержки определяется волновым сопротивлением Z0 и временем задержки TD. Значение волно-вого сопротивления роли не играет, пока линия нагружена на сопротивление, равное волновому. Параметр задержки TD определяет интервал осуществления выборки сигнала в ЦФ или частоту дискретизации FC. Источники на входе отрезков линии передачи – это зависимые ИНУН (см. п. 3.1) с коэффициентом передачи, равным 1. Эти источники играют роль буферов, разделяющих после-довательно включённые элементы задержки.
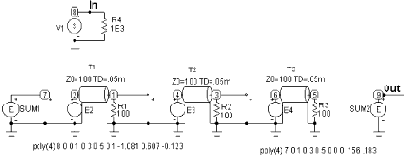
Рис. 6.9
На вход фильтра включён такой же источник V1, как и на вход фильтра первого примера (см. Рис. 6.1 и Рис. 6.2). Два сумматора структурной схемы Рис. 6.8 выполнены на нелинейных зависимых источниках напряжения, управлямых напряжением (см. п. 3.2 и Рис. 3.7). Для правильного сумми-рования сигналов в соответствии с Рис. 6.8 нужно правильно определить атрибуты этих источников. Окно атрибутов источника SUM1 показано на Рис. 6.10, а источника SUM2 – на Рис. 6.11.
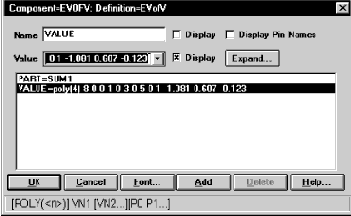
Рис. 6.10
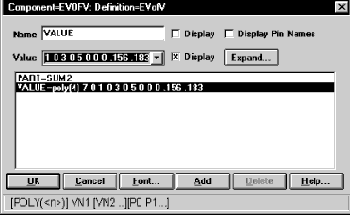
Рис. 6.11
На Рис. 6.12 приведено окно пределов анализа фильтра во временной области, а на Рис. 6.13 – результаты этого анализа. В форме выходного сигнала на Рис. 6.13 характерно выделяются перепады напряжения на интервалах времени, длительностью 50 мс.
На Рис. 6.14 приведено окно пределов анализа фильтра в частотной области, а на Рис. 6.15 – результаты расчёта АЧХ рассматриваемого фильтра.
Из Рис. 6.15 виден очень характерный для фильтров этого типа момент – периодическое повторение АЧХ фильтра через 20 кГц, которое соответствуют частоте дискретизации фильтра.
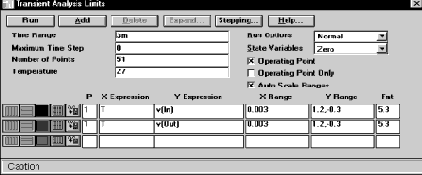
Рис. 6.12
Принципиальная схема фильтра, соответствующая Рис. 6.8, показана на Рис. 6.9. Отрезок идеальной линии передачи на Рис. 6.9 соответствует элементу z-1 на Рис. 6.8 и в системной функции (6.1) фильтра. Линия задержки определяется волновым сопротивлением Z0 и временем задержки TD. Значение волно-вого сопротивления роли не играет, пока линия нагружена на сопротивление, равное волновому. Параметр задержки TD определяет интервал осуществления выборки сигнала в ЦФ или частоту дискретизации FC. Источники на входе отрезков линии передачи – это зависимые ИНУН (см. п. 3.1) с коэффициентом передачи, равным 1. Эти источники играют роль буферов, разделяющих после-довательно включённые элементы задержки.

