Общие положения
При анализе и синтезе дискретных и цифровых устройств широко используется Z – преобразование, играющее по отношению к дискретным сигналам такую же роль, как преобразования Фурье и Лапласа по отношению к непрерывным сигналам [11]. Весьма широко и конструктивно с использовани-ем Z – преобразования проводится синтез цифровых фильтров, а реализация их осуществляется и программно [12]. Использование ПЭВМ и ССМ, содержащих аппарат преобразования Лапласа, например, МС5, позволяет проводить машинное моделирование дискретных систем типа фильтров с переключаемыми конденсаторами и цифровых фильтров на отрезках длинных линий. Важность этого момента для учебных целей очевидна.
В формате SPICE нет источника, реализующего Z преобразование. Поэтому в MC5 версии 2 вводится собственный формат для линейных зависимых источников, задаваемых Z – преобразованием с использованием выражения от комплексной переменной Z. Описание этих источников было приведено в п. 3.5 пособия.
Z - преобразование задается следующим уравнением:
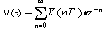
где: z-n - оператор задержки, n - число единичных задержек, T - интервал осуществления выборки и V(nT) - дискретные аналоговые выборки. Это уравнение не может быть вычислено непосредственно в MC5. Но в MC5 можно провести эквивалентное преобразование по Лапласу. С использованием источника, задаваемого преобразованием Лапласа, любые функции Z - преобразования могут быть переведены в функции преобразования по Лапласу через замену: Z = e sT. Но в МС5 пользователь работает непосредственно с выражениями от переменной z. Рассмотрим два основных примера.
